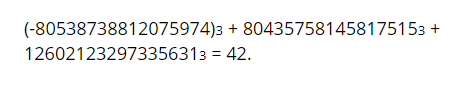Matematikçiler en sonunda küplerinin toplamı 42’yi veren üç sayıyı buldu. Böylece 65 yıl önce ortaya atılan ve 100’den küçük doğal sayıların hepsinin üç tam sayının küpleri şeklinde yazılıp yazılamayacağı sorusunun cevabı tamamlanmış oldu.

İlk kez 1954’te ortaya konan problem çok basit bir eşitliğe cevap arıyor: x3+y3+z3=k. Soru 1’le 100 arasındaki tüm sayılar için x, y ve z bilinmeyenlerinin alması gereken değerleri arıyor.

İlk zamanlar daha kolay sayılar için cevap bulunmuştu ve 2000’de Harvard Üniversitesi’nden matematikçi Noam Elkies daha zor sayıların bulunmasına yardım edecek bir algoritma geliştirmişti.

2019’a kadar diğer tüm sayılar için olumlu ve olumsuz cevaplar bulunmuş ve geriye iki sayı kalmıştı: 33 ve 42.

YouTube’da “Numberphile” isimli popüler matematik kanalının 33 problemiyle ilgili videosu, Bristol Üniversitesi’nden matematikçi Andrew Booker’a yeni bir algoritma yazmak için ilham vermişti.

Üniversitenin güçlü bir süperbilgisayarını kullanan Brooker 33 problemine sadece üç hafta içinde cevap bulmuş ve geriye sadece en zor olanı, yani 42 kalmıştı.

42 sayısı çok daha inatçı bir problem olduğunu ispatlamıştı ve bu nedenle Brooker, büyük ölçekte paralel bilgi işlemede uzman, Massachusetts Teknoloji Enstitüsü’den (MIT) Andrew Sutherland’in yardımına başvurdu.

Science Alert’in haberine göre matematikçiler sadece cevabı bulmakla kalmadı, kişisel internet sitelerini güncelleyerek başlığa “Hayat, Evren ve Her Şey” ismini verdi ve Douglas Adams’a gönderme yaptı.

Douglas Noel Adams’ın Otostopçu'nun Galaksi Rehberi’nde “hayat, evren ve her şeye dair nihai sorunun cevabının” 42 olduğu biliniyor ama sorunun ne olduğu bilinmiyor. Bu yüzden soruyu hesaplamak için organik bir bilgisayar olarak Dünya inşa ediliyor.

Matematikçiler de romana benzer şekilde yüksek işlem gücü gerektiren bu soruyu hesaplamak için 500 bin ev bilgisayarından güç alan bir tür “gezegensel süperbilgisayar” kullandı.

Klasik bilgisayarların milyonlarca saat çalışmasını gerektiren süreç sonunda matematikçiler “soruyu” buldu:

Brooker konuyla ilgili şunları ifade etti:

Bu oyunda, bir şeyler bulacağınızdan emin olmanız imkansızdır. Biraz depremleri öngörmeye benziyor, bu (süreçte) elimizde sadece kabataslak olasılıklar vardı. Bu yüzden, birkaç aylık araştırma sonucunda aradığımız şeyi bulabilir ya da bir yüz yıl daha bulamayabilirdik.

Peki her şey son buldu mu? Hayır, çünkü sadece 1’le 100 arasındaki sayılar tamamlandı, 1000’e kadar olan pek çok sayı hala “sorusunun” hesaplanmasını bekliyor: 114, 165, 390, 579, 627, 633, 732, 906, 921 ve 975.

Science Alert

Independent Türkçe için çeviren: Umut Can Yıldız